האפעה ברנט-קונג הוצעה בשנת 1982 על ידי Hsiang Te Kung & Richard Peirce Brent. זהו מוסיף קידומת מקביל או מוסיף עצים שנמצא בשימוש נרחב בעיצוב דיגיטלי בשל הגמישות שלו. ניתן לבנות מוסיף קידומת מקביל בכמה דרכים בהתבסס על מספר רמות ההיגיון, שערים לוגיים מעורב, המניפה מכל שער והחיווט בין הרמות. ישנם סוגים שונים של מוסיף עצים זמינים, מוסיף העץ הבסיסי הם Sklanskym KoggeStone & Brent-Kung, בהשוואה ל-KSA (Kogge–Stone Adder), מוסיף זה מספק סדירות גבוהה למבנה האפעף ויש לו פחות חסימת חיווט מה שמוביל לביצועים טובים יותר ופחות שטח שבב נדרש. מאמר זה מספק מידע קצר על א ברנט קונג אדדר .
מה זה ברנט קונג אדדר?
מוסיף שמשתמש במעגלים מינימליים כדי לקבל את התוצאה ידוע בשם Brent Kung Adder והוא ידוע גם בתור מוסיף בעל הספק נמוך או מוסיף מקביל. האפעה הזו נועדה לחסוך בגודל השבב כך שייצור האפיחות הללו יהפוך לקל יותר. הסימטריה ומבנה הבנייה הרגיל של האפעה הזה יפחיתו מאוד את עלויות הייצור ואפשר להשתמש בטופולוגיות בצנרת. השימוש בלוגיקה של טרנזיסטור מעבר משלים עוזר בשיפור ביצועי התכנון עם ה- מרובה גישה בעיצובי תאים שונים.
מעגל ברנט קונג אדדר
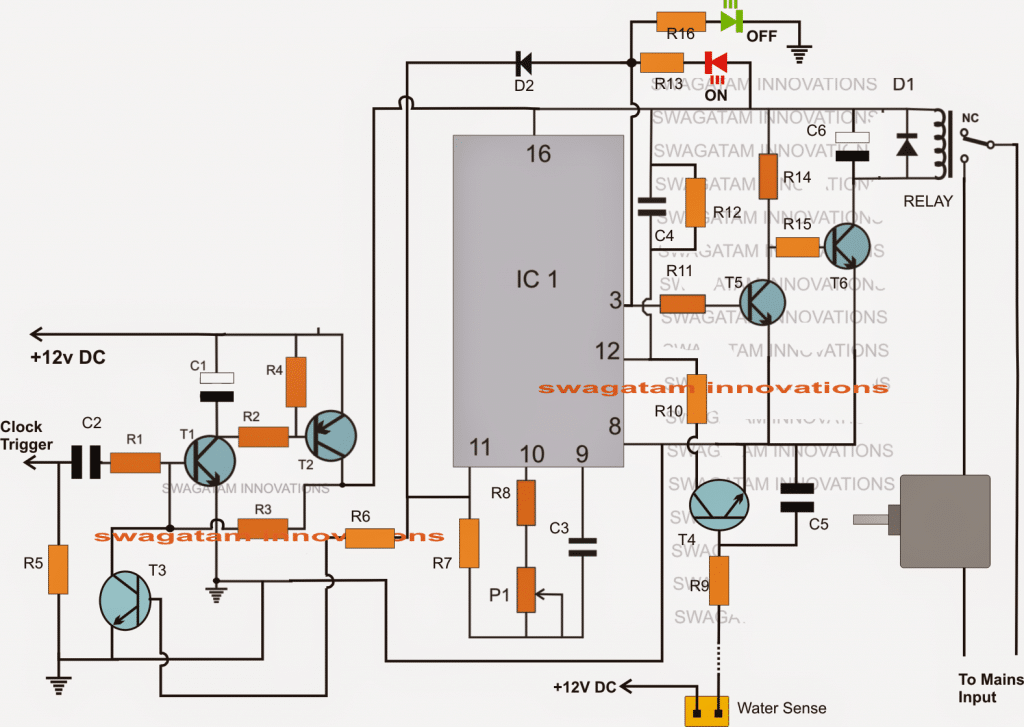
דיאגרמת מוסיף הקידומת המקבילה של ברנט-קונג מוצגת להלן הכוללת את שלב 1 (שלב עיבוד מוקדם), שלבים 2 עד 7 הם שלבי יצירת העברה ושלב 8 הוא שלאחר עיבוד. זוהי ארכיטקטורה מתקדמת ופשוטה מאוד לבנייה ומספקת פחות גודש בחיווט. אז, פחות החיווט שלו יקטין את כמות השטח הנדרש לביצוע הארכיטקטורה. בנוסף, הניתוב הופך להרבה יותר קל בגלל חציית (או) חפיפה של פחות חוטים. עם זאת, העונש יגדל בעיכוב בגלל מספר השלבים המוגדל, יציאת המאוורר עבור מוסיף זה גדל, ואז העיכוב יגדל.

כיצד פועל ברנט קונג אדדר?
Brent Kung Adder פועל על ידי חישוב הקידומות עבור שתי קבוצות סיביות אשר שימושיות במציאת קידומות קבוצת 4 סיביות. קידומות אלו משמשות לחישוב הקידומות של קבוצת 8 סיביות וכו'. לאחר מכן, הקידומות הללו ישמשו לחישוב הביצוע של שלב הסיביות הספציפי. תאריכים אלה משמשים עם תפוצת הקבוצה של השלב הבא כדי לחשב את סיביות הסכום של אותו שלב. Brent Kung Tree משתמש ב-2log2N – שלב אחד.
ברנט קונג אדדר 32 סיביות
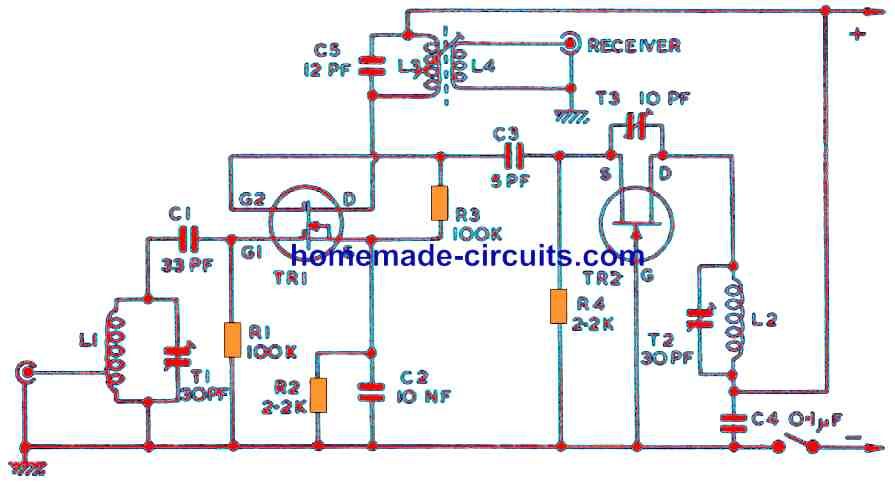
פריסת ה-Brent Kung של 32 סיביות מוצגת להלן. בתחילת הפריסה הזו, שערי לוגיקה בסיסיים מתוכננים כמו NAND, מהפך, XOR, NOR וכו'. לאחר מכן, התאים הדרושים כמו תאים שחורים, תאים אפורים, חוצצים והיגיון PG מתוכננים עם השערים הלוגיים.

באדר ברנט קונג שלמטה 32 סיביות, השערים ההפוכים כמו AOI ו-OAI משמשים לחילופין בעיקר עבור תאים אפורים ושחורים. אז התאים השחורים והאפורים מיוצגים עם בלוקים אפורים ושחורים בעוד שהמאגרים מיוצגים עם עיגולים.


הכניסות כמו A & B מסופקות ללוגיקה של PG שמוצגת בתרשים הבלוק. עבור מוסיף 32 סיביות, נחוצים 32 בלוקים לוגיים של PG ואותות ההפצה (P) ויצירת (G) הם הפלטים של בלוק זה. האותות הללו מסופקים למבנה עץ האפעה של ברנט קונג. המבנה של מוסיף זה כולל תאים אפורים ותאים שחורים.
תא אפור כולל שלוש כניסות ופלט בודד. ההפצה וההפקה של האותות מהשלב הנוכחי ויצירת אותות מהשלב הקודם הם כניסות ואילו הקבוצה יוצרת אותות היא ה-o/p. בכל מבנה עץ, כל שלב יסתיים בתא אפור וה-o/p של התא הזה הוא האות של יצירת הקבוצה. אות זה נחשב פשוט כנושא של אותו שלב. התא השחור כולל ארבע כניסות ושתי יציאות. הכניסות לתא זה הן אותות P & G של השלב הנוכחי & אותות P, G מהשלב הקודם.
לוגיקה PG כוללת שערי AND & XOR כאשר השער הלוגי AND משמש להפקת אות G ושער לוגי XOR מספק את אות P. כדי למנוע ממירים מיותרים, משתמשים בשני סוגים של תאים אפורים ותאים שחורים. השערים ההפוכים המשמשים בשורה אחת עבור התא האפור הם AOI או AND-OR-Inverter והשערים ההפוכים עבור התא השחור בשורה הבאה משתמשים ב-OAI או OR-AND-Inverter. תא AOI משתמש בכניסות הרגילות כדי לספק יציאות הפוכות ואילו OAI משתמש בכניסות הפוכות כדי לספק יציאות רגילות.
מבצע ברנט קונג אדדר
מוסיף ברנט קונג הוא מוסיף קידומת מקביל המשמש להפעלת הוספה בעלת ביצועים גבוהים. האפעף הזה נראה כמו מבנה עץ שמבצע את הפעולה האריתמטית. מוסיף זה כולל תאים שחורים ותאים אפורים. לכל תא שחור יש שני שערי AND ושער OR יחיד ולכל תא אפור יש רק שער AND בודד.
האפען ברנט-קונג כולל שני שלבים; שלב העיבוד המקדים ושלב הדור. בשלב הראשון, ההפקה וההפצה יהיו מכל זוג תשומות. כאן ה-propagate מספק פעולת 'XOR' עבור סיביות קלט ואילו יוצר מספק פעולת 'AND' עבור סיביות קלט. להפיץ וליצור כמו 'Pi' ו-'Gi' ניתנים להלן.
Pi = Ai XOR Bi ו- Gi = Ai AND Bi.
בשלב השני, ה-carry ייווצר עבור כל סיביות שידוע בתור carry genereer 'Cg' ו-carry is propagate עבור כל סיביות ידוע כ-carry gener 'Cp'. לפעולה נוספת, יווצרו carry propagate & carry gener. התא הסופי זמין בכל חלק לפעול מספק נשיאה. אז העברת הסיביות האחרונה תסייע לסכום הסיביות הבאות במקביל עד הסיביות האחרונה. ה- carry gener & propagate ניתנים בתור;
Cp = P1 ו-P0 ו-Cg=G1 OR (P1 ו-G0)
הוא משמש בעיקר עבור פעולת הוספה של שני שלושים ושתיים ביטים וכל סיביות חווה את שלב העיבוד המקדים ושלב היצירה ואז הוא מספק את הסכום הסופי.
סיביות הקלט העיקריות עוברות מתחת לשלב העיבוד המקדים והן מייצרות התפשטות ויצירת. אז אלה מתפשטים כמו גם מייצרים עוברים שלב הייצור מייצרים תפוצה מובילה ומספקת סכום סופי. תהליך האפעה של ברנט-קונג שלב אחר שלב מוצג להלן.

סידור האפעף ברנט-קונג נראה כמו מבנה עץ והוא האפעף המהיר שמכוון ללוגיקה ברמת השער. ניתן לעצב את האפעה הזו עם ירידה במספר השערים הלוגיים. לפיכך, זה מפחית את ההשהיה והזיכרון המשמשים בארכיטקטורה זו.
Brent Kung Adder Code Verilog
קוד verilog של Brent Kung Adder מוצג להלן.
`הגדר INPUTSIZE 64 //הגדר את גודל הקלט n
`הגדר GROUPSIZE 8 //הגדר את גודל הקבוצה = 1, 2, 4 או 8
מודול Brent_Kung_Adder(A, B, S);
קלט [`INPUTSIZE – 1:0] א;
קלט [`INPUTSIZE – 1:0] ב;
פלט [`INPUTSIZE:0] S;
wire [`INPUTSIZE / `GROUPSIZE * 2 – 1:0] r_temp;
חוט [`INPUTSIZE / `GROUPSIZE * 2 – 1:0] r;
wire [`INPUTSIZE / `GROUPSIZE:0] cin;
wire [`INPUTSIZE / `GROUPSIZE * 2 – 1:0] q;
הקצה cin[0] = 1'b0;
לִיצוֹר
איפה ב;
עבור (i = 0; i < `INPUTSIZE / `GROUPSIZE; i = i + 1) מתחילים: parallel_FA_CLA_prefix
group_q_generation #(.Groupsize(`GROUPSIZE))
f(
.a(A[`GROUPSIZE * (i + 1) – 1:`GROUPSIZE * i]),
.b(B[`GROUPSIZE * (i + 1) – 1:`GROUPSIZE * i]),
.cin(cin[i]),
.s(S[`GROUPSIZE * (i + 1) – 1:`GROUPSIZE * i]),
.qg(q[i * 2 + 1:i * 2])
);
סוֹף
parallel_prefix_tree_first_half #(.Treesize(`INPUTSIZE / `GROUPSIZE))
t1(
.q(q[`INPUTSIZE / `GROUPSIZE * 2 – 1:0]),
.r(r_temp[`INPUTSIZE / `GROUPSIZE * 2 – 1:0])
);
parallel_prefix_tree_second_half #(.Treesize(`INPUTSIZE / `GROUPSIZE))
t2(
.q(r_temp[`INPUTSIZE / `GROUPSIZE * 2 – 1:0]),
.r(r[`INPUTSIZE / `GROUPSIZE * 2 – 1:0])
);
עבור (i = 0; i < `INPUTSIZE / `GROUPSIZE; i = i + 1) מתחילים: cin_generation
cin_generation_logic f(
.r(r[2 *i + 1:2 *i]),
.c0(1'b0),
.cin(cin[i + 1])
);
סוֹף
הקצה S[`INPUTSIZE] = cin[`INPUTSIZE / `GROUPSIZE];
להפיק סוף
endmodule
// המחצית הראשונה של עץ הקידומת המקבילה
module parallel_prefix_tree_first_half #(פרמטר Treesize = `INPUTSIZE / `GROUPSIZE)(q,r);
קלט [Treesize * 2 – 1:0] q;
פלט [גודל עץ * 2 – 1:0] r;
לִיצוֹר
איפה ב;
if (Treesize == 2) מתחילים: trivial_case
הקצה r[1:0] = q[1:0];
prefix_logic f(
.ql(q[1:0]),
.qh(q[3:2]),
.r(r[3:2])
);
סוף אחר להתחיל: רקורסיבי_מקרה
חוט [Treesize * 2 – 1:0] r_temp;
parallel_prefix_tree_first_half #(.Treesize(Treesize / 2))
recursion_lsbh(
.q(q[Treesize – 1:0]),
.r(r_temp[Treesize – 1:0])
);
parallel_prefix_tree_first_half #(.Treesize(Treesize / 2))
recursion_msbh(
.q(q[Treesize * 2 – 1:Treesize]),
.r(r_temp[Treesize * 2 – 1:Treesize])
);
עבור (i = 0; i < Treesize * 2; i = i + 2) מתחילים: parallel_stitch_up
if (i != Treesize * 2 – 2) מתחילים: parallel_stitch_up_pass
הקצה r[i + 1:i] = r_temp[i + 1:i];
סוף אחר להתחיל: parallel_stitch_up_produce
prefix_logic f(
.ql(r_temp[Treesize – 1:Treesize – 2]),
.qh(r_temp[Treesize * 2 – 1:Treesize * 2 – 2]),
.r(r[Treesize * 2 – 1:Treesize * 2 – 2])
);
סוֹף
סוֹף
סוֹף
להפיק סוף
endmodule
// המחצית השנייה של עץ הקידומת המקבילה
module parallel_prefix_tree_second_half #(פרמטר Treesize = `INPUTSIZE / `GROUPSIZE)(q, r);
קלט [Treesize * 2 – 1:0] q;
פלט [גודל עץ * 2 – 1:0] r;
wire [Treesize * 2 * ($clog2(Treesize) – 1) – 1:0] r_temp;
הקצה r_temp[Treesize * 2 – 1:0] = q[Treesize * 2 – 1:0];
לִיצוֹר
גנוואר א, י;
עבור (i = 0; i < $clog2(Treesize) – 2; i = i + 1) begin: second_half_level
הקצה r_temp[Treesize * 2 * (i + 1) + ((Treesize / (2 ** i)) – 1 – 2 ** ($clog2(Treesize / 4) – i)) * 2 – 1:Treesize * 2 * (i + 1)] = r_temp[Treesize * 2 * i + ((Treesize / (2 ** i)) – 1 – 2 ** ($clog2(Treesize / 4) – i)) * 2 – 1: גודל עץ * 2 * i];
עבור (j = (Treesize / (2 ** i)) – 1 – 2 ** ($clog2(Treesize / 4) – i); j < Treesize; j = j + 2 ** ($clog2(Treesize / 2 ) – i)) begin: second_half_level_logic
prefix_logic f(
.ql(r_temp[Treesize * 2 * i + (j – 2 ** ($clog2(Treesize / 4) – i)) * 2 + 1:Treesize * 2 * i + (j – 2 ** ($clog2( גודל עץ / 4) – i)) * 2]),
.qh(r_temp[Treesize * 2 * i + j * 2 + 1:Treesize * 2 * i + j * 2]),
.r(r_temp[Treesize * 2 * (i + 1) + j * 2 + 1:Treesize * 2 * (i + 1) + j * 2])
);
if (j != Treesize – 1 – 2 ** ($clog2(Treesize / 4) – i)) begin: second_half_level_direct_connect
הקצה r_temp[Treesize * 2 * (i + 1) + (j + 2 ** ($clog2(Treesize / 2) – i)) * 2 – 1:Treesize * 2 * (i + 1) + j * 2 + 2] = r_temp[Treesize * 2 * i + (j + 2 ** ($clog2(Treesize / 2) – i)) * 2 – 1:Treesize * 2 * i + j * 2 + 2];
סוֹף
סוֹף
הקצה r_temp[Treesize * 2 * (i + 2) – 1:Treesize * 2 * (i + 2) – (2 ** ($clog2(Treesize / 4) – i)) * 2] = r_temp[Treesize * 2 * (i + 1) – 1:Treesize * 2 * (i + 1) – (2 ** ($clog2(Treesize / 4) – i)) * 2];
סוֹף
הקצה r[1:0] = r_temp[Treesize * 2 * ($clog2(Treesize) – 2) + 1:Treesize * 2 * ($clog2(Treesize) – 2)];
עבור (i = 1; i < Treesize; i = i + 2) begin: final_r_odd
הקצה r[i * 2 + 1:i * 2] = r_temp[Treesize * 2 * ($clog2(Treesize) – 2) + i * 2 + 1:Treesize * 2 * ($clog2(Treesize) – 2) + i * 2];
סוֹף
עבור (i = 2; i < Treesize; i = i + 2) begin: final_r_even
prefix_logic f(
.ql(r_temp[Treesize * 2 * ($clog2(Treesize) – 2) + i * 2 – 1:Treesize * 2 * ($clog2(Treesize) – 2) + i * 2 – 2]),
.qh(r_temp[Treesize * 2 * ($clog2(Treesize) – 2) + i * 2 + 1:Treesize * 2 * ($clog2(Treesize) – 2) + i * 2]),
.r(r[i * 2 + 1:i * 2])
);
סוֹף
להפיק סוף
endmodule
module group_q_generation #(parameter Groupsize = `GROUPSIZE)(a, b, cin, s, qg);
קלט [גודל קבוצתי – 1:0] a;
קלט [גודל קבוצתי – 1:0] ב;
קלט cin;
פלט [גודל קבוצתי - 1:0] s;
פלט [1:0] qg;
חוט [2 * גודל קבוצה - 1:0] ש;
חוט [גודל קבוצתי – 1:0] ג;
הקצה c[0] = cin;
לִיצוֹר
איפה ב;
עבור (i = 0; i < גודל קבוצה; i = i + 1) מתחיל: parallel_FA_CLA_prefix
FA_CLA_prefix f(
.a(a[i]),
.b(b[i]),
.cin(c[i]),
.s(s[i]),
.q(q[i * 2 + 1:i * 2])
);
if (i != Groupsize – 1) begin: special_case
הקצה c[i + 1] = q[i * 2 + 1] | (q[i * 2] & c[i]);
סוֹף
סוֹף
// group q דור המבוסס על Groupsize
if (גודל קבוצתי == 1) מתחיל: case_gs1
הקצה qg[1] = q[1];
הקצה qg[0] = q[0];
end else if (Groupsize == 2) begin: case_gs2
הקצה qg[1] = q[3] | (q[1] & q[2]);
הקצה qg[0] = q[2] & q[0];
end else if (קבוצתיות == 4) begin: case_gs4
הקצה qg[1] = q[7] | (ש[5] ו-ש[6]) | (q[3] & q[6] & q[4]) | (q[1] & q[6] & q[4] & q[2]);
הקצה qg[0] = q[6] & q[4] & q[2] & q[0];
end else if (קבוצתיות == 8) begin: case_gs8
הקצה qg[1] = q[15] | (ש[13] ו-ש[14]) | (q[11] & q[14] & q[12]) | (q[9] & q[14] & q[12] & q[10]) | (q[7] & q[14] & q[12] & q[10] & q[8]) | (q[5] & q[14] & q[12] & q[10] & q[8] & q[6]) | (q[3] & q[14] & q[12] & q[10] & q[8] & q[6] & q[4]) | (q[1] & q[14] & q[12] & q[10] & q[8] & q[6] & q[4] & q[2]);
הקצה qg[0] = q[14] & q[12] & q[10] & q[8] & q[6] & q[4] & q[2] & q[0];
סוֹף
להפיק סוף
endmodule
// היגיון יצירת Cin
מודול cin_generation_logic(r, c0, cin);
קלט [1:0] r;
קלט c0;
פלט cin;
הקצה cin = (r[0] & c0) | r[1];
endmodule
// לוגיקה בסיסית לפעולות קידומת
module prefix_logic(ql, qh, r);
קלט [1:0] ql;
קלט [1:0] qh;
פלט [1:0] r;
הקצה r[0] = qh[0] & ql[0];
הקצה r[1] = (qh[0] & ql[1]) | qh[1];
endmodule
// תא Adder מלא עם Carry Look-Ahead
מודול FA_CLA_prefix(a, b, cin, s, q);
קלט a;
קלט b;
קלט cin;
פלט s;
פלט [1:0] q;
הקצה q[0] = a ^ b;
הקצה s = q[0] ^ cin;
הקצה q[1] = a & b;
endmodule
יתרונות
היתרונות של ברנט קונג אדדר כוללים את הדברים הבאים.
- זהו מוסיף בעל הספק נמוך מכיוון שהוא משתמש במעגל מינימלי כדי לקבל את התוצאה.
- זה מאוד פופולרי & בשימוש נרחב.
- ניתן ליישם סוג זה של מוסיף על ידי שימוש בפחות מודולים בהשוואה ל-Kogge-Stone מוסיף.
- עיצוב אדות ברנט-קונג קל מאוד.
- למוסיף זה יש פחות חיבורים עם מודולים אחרים.
- האפעות הללו הוצעו בעיקר כדי לפתור את החסרונות של אדפי קוגה-סטון.
חסרונות
ה החסרונות של ברנט קונג אדה r כלול את הדברים הבאים.
- למוספים האלה יש השהייה גדולה יותר והם צריכים 2 log2 n - 2 רמות לוגיות לחישוב כל סיביות ה-carrier.
- החיסרון העיקרי של מוסיף זה הוא תנודות שיכולות לגרום להתפשטות הזרם בכל האפעף להתפצל ולהיחלש.
יישומי Brent Kung Adder
היישומים של Brent Kung Adder כוללים את הדברים הבאים.
- באדר ברנט-קונג נעשה שימוש בצינור כדי להפחית את צריכת החשמל על ידי הפחתת עומק ההיגיון הקומבינטורי וייצוב התקלות.
- אדר ברנט-קונג מספק מספר יוצא מן הכלל של שלבים מ-i/p ועד כל o/ps אך עם טעינת שלבי ביניים אסימטרית.
- ניתן להשתמש במוסיף זה בתוך המכפיל כמו גם ברכיבי נתיב נתונים אחרים.
לפיכך, זהו סקירה כללית של ברנט קונג אדדר , פעולתו, היתרונות, החסרונות והיישומים שלו. מדובר באפעה יעילה מאוד והמבנה שלו נראה כמו מבנה עץ המשמש בעיקר לפעולות אריתמטיות בעלות ביצועים גבוהים. סוג זה של מוסיף מהיר מאוד ומתמקד בעיקר בלוגיקה ברמת השער. מוסיף זה מתוכנן על ידי שימוש במספר קטן יותר של שערים לוגיים. לפיכך, זה מקטין את הזיכרון והעיכוב בשימוש בארכיטקטורה זו. הנה שאלה בשבילך, ברנט קונג אדדר הידוע גם בשם?